ΘΕΜΑ Α
Α1. Να αποδείξετε ότι η παράγωγος της ταυτοτικής συνάρτησης f(x) x = είναι f (x) (x) 1 ′ = ′ = για κάθε x στο σύνολο των πραγματικών αριθμών. Μονάδες 10
Α2. Να δώσετε τον ορισμό της διαμέσου (δ) ενός δείγματος ν παρατηρήσεων, όταν το ν είναι περιττός αριθμός. Μονάδες 5 Α3.
Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή ή τη λέξη Λάθος, αν η πρόταση είναι λανθασμένη.
α) ( )′ ημx =συνx (Μον. 2)
β) ( )′ = 1 3 2 3 (Μον. 2)
γ) Σε μία κανονική ή περίπου κανονική κατανομή στο διάστημα ( ) x ,x − + s s βρίσκεται το 68% περίπου των παρατηρήσεων. (Μον. 2)
δ) Αν 0 1 x x lim f(x) → = A και 0 2 x x lim g(x) → = A όπου A A, 1 2 πραγματικοί αριθμοί τότε: ( ) → = 0 1 2 x x lim f(x) g(x) . A A (Μον. 2
ε) Μια συνάρτηση f λέγεται γνησίως αύξουσα σε ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε σημεία 1 2 x ,x ∈Δ με 1 2 x x < ισχύει 1 2 f(x ) f(x ) < . (Μον. 2) Μονάδες 10
ΘΕΜΑ Β
Στον παρακάτω πίνακα δίνεται ο αριθμός των πιστωτικών καρτών που έχουν 20 υπάλληλοι μιας επιχείρησης. Αριθμός πιστωτικών καρτών i x Αριθμός υπαλλήλων i ν Αθροιστική Συχνότητα Ni Σχετική Συχνότητα i f % i i x ν 0 5 1 9 2 10 3 4 ΣΥΝΟΛΑ
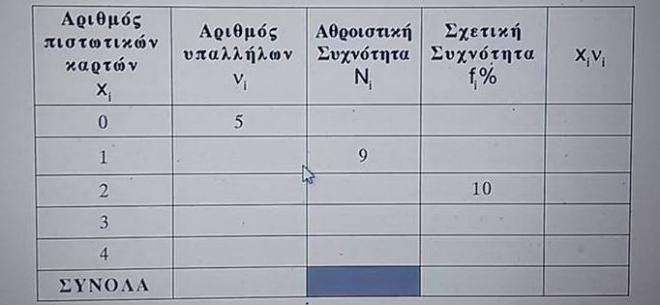
Β1. Αν γνωρίζετε ότι η 5η συχνότητα 5 ( ) ν ισούται με την 1η συχνότητα 1 ( ) ν , να μεταφέρετε στο τετράδιό σας τον παραπάνω πίνακα και να τον συμπληρώσετε. Μονάδες 10 Β2. Να υπολογίσετε τη μέση τιμή x των πιστωτικών καρτών των υπαλλήλων. Μονάδες 5
Β3. Να υπολογίσετε τον αριθμό των υπαλλήλων που έχουν το πολύ 3 πιστωτικές κάρτες. Μονάδες 5
Β4. Να υπολογίσετε το ποσοστό των υπαλλήλων που έχουν τουλάχιστον 2 πιστωτικές κάρτες. Μονάδες 5
ΘΕΜΑ Γ
∆ίνεται η συνάρτηση f : → με τύπο: = + + 2 x 1 f(x) x 12
Γ1. Να αποδείξετε ότι ( ) − ′ = + 2 2 2 1 x f (x) x 1 Μονάδες 6
Γ2. Να βρείτε το ρυθμό μεταβολής της συνάρτησης f στα σημεία 1 x 1 = − και 2 x 1= . Μονάδες 4
Γ3. Να μελετήσετε τη συνάρτηση f ως προς τη μονοτονία και να βρείτε τα τοπικά της ακρότατα. Μονάδες 12
Γ4. Να συγκρίνετε τις τιμές f(2015) και f(2016) της συνάρτησης f . Μονάδες 3
ΘΕΜΑ ∆
∆ίνεται η συνάρτηση f : → με τύπο: =+ − ∈ 2 f(x) x αx 3, α .
∆1. Να υπολογίσετε την τιμή του α αν 2 x 4 x 6x 8 α =lim → x 4 − + − Μονάδες 8
∆2. Για α=2 να βρείτε την f (x). ′ Μονάδες 3
∆3. Για α=2 να βρείτε την εξίσωση της εφαπτομένης της γραφικής παράστασης της συνάρτησης f στο σημείο M 2,f( 2) ( ) − − .
∆4. Αν τα σημεία A111 2 2 2 3 3 3 4 4 4 5 5 5 (x ,y ), A (x ,y ), A (x ,y ), A (x ,y ), A (x ,y ) ανήκουν στην ευθεία ε: y 2x 7 = − − και οι τετμημένες 123 45 x,x,x,x,x των σημείων A1 2345 , A ,A ,A ,A έχουν μέση τιμή x 2 = , να βρείτε τη μέση τιμή y των τεταγμένων 123 45 y,y,y,y,y των σημείων αυτών. Μονάδες 6
ΔΕΙΤΕ ΟΛΕΣ ΤΙΣ ΑΠΑΝΤΗΣΕΙΣ ΕΔΩ







